Self Organizing Map (or Kohonen Map or SOM) is a type of Artificial Neural Network. It follows an unsupervised learning model. It also represents the clustering concept by grouping similar data together. It is a technique to map multidimensional data onto lower-dimensional which allows people to reduce complex problems for easy interpretation.
It calculates the closest distance between the input vector & output vectors
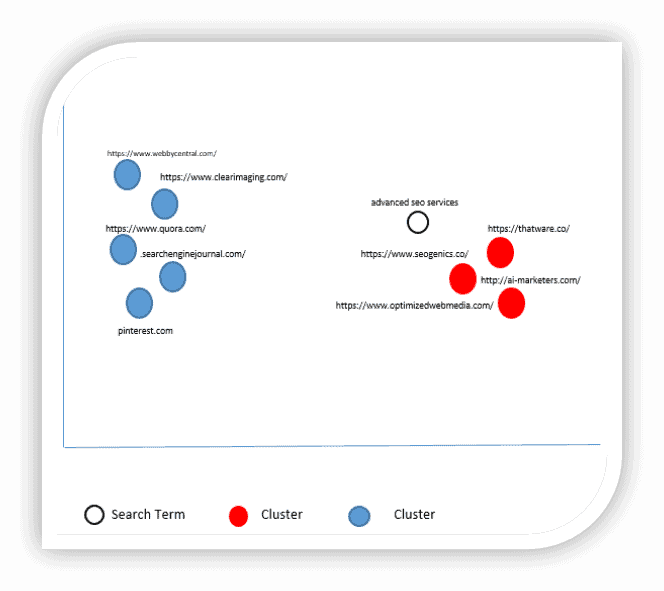
Here we have to calculate a closer campaign according to the search term & we can easily find who are our top competitors. This program will help us find the actual competitors of our campaign & after finding the competitors; we can optimize our landing page’s properly for SERP improvements.
Kohonen self organizing map Algorithm
Each node weight initialize to a random value.
Choose a random input vector
Calculate the Euclidean distance between weight vector wij and the input vector x(t) connected with the first node, where t, i, j =0.
Track the node that generates the smallest distance t.
Calculate the overall Best Matching Unit (BMU). It means the node with the smallest distance from all calculated ones.
Discover the topological neighbourhood βij(t) and its radius σ(t) of BMU in the Kohonen Map.
Repeat for all nodes in the BMU neighbourhood: Update the weight vector w_ij of the first node in the neighbourhood of the BMU by including a fraction of the difference between the input vector x(t) and the weight w(t) of the neuron.
Repeat the complete iteration until reaching the selected iteration limit t=n.
Here, step 1 represents the initialization phase, while step 2 to 9 represents the training phase.
Where;
t = current iteration.
i = row coordinate of the nodes grid.
J = column coordinate of the nodes grid.
W= weight vector
w_ij = association weight between the nodes i,j in the grid.
X = input vector
X(t)= the input vector instance at iteration t
β_ij = the neighbourhood function, decreasing and representing node i,j distance from the BMU.
σ(t) = The radius of the neighbourhood function, which calculates how far neighbour nodes are examined in the 2D grid when updating vectors. It gradually decreases over time.
